FPGA Lesson 2 ─ 組合邏輯電路描述方法差異

前言

組合邏輯電路的特點是：電路中任意時刻的穩態狀態只取決於該時刻的輸入，與原電路的現態無關。相比於順序邏輯電路的特點是： 電路中任意時刻的穩態狀態「不」只取決於該時刻的輸入也與原電路的現態有關。

組合邏輯電路

設計一個組合邏輯電路的考量

• 所用的邏輯單元(Logic cell)數量最少，使用模組最少，模組與模組連接(wire)最簡化，這樣地電路被我們稱為＂最小化＂電路。
• 為了滿足工作頻率的要求，多級的電路應當避免，減少閘與閘之間的延遲，同時電路的功耗也要盡量地小。

組合電路的三種描述方法

• 結構描述(Structure description)
• 邏輯代數(Boolean algebra)
• 抽象描述(abstract description)

舉例：三人裁判電路

以下舉例一個三人裁判電路，也就是ABC三個人只要有大於一人的情況，輸出就會為真。可以從下圖真值表看到。

• 

以下是直接真值表轉化出來的RTL View，可以看到未經化簡的真值表，做出來的電路不符合我們上述提到的＂最小化＂電路的設定，所以以下介紹三種不同的描述方式。

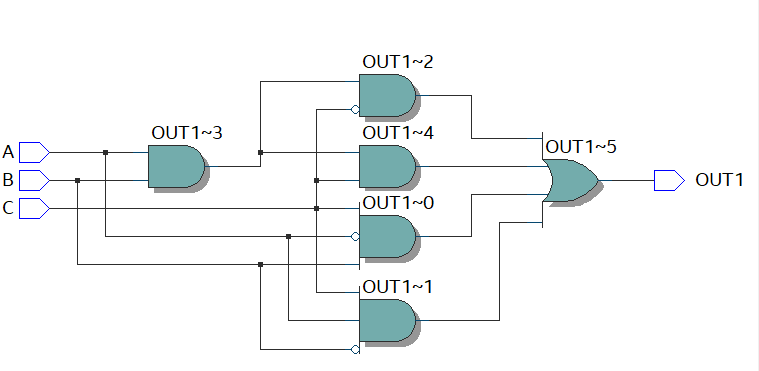
結構描述(Structure description)

結構描述是一個語法轉化最簡電路的方式，相比於直接用真值表寫電路，或是用真值表轉卡諾圖化簡， 結構描述比較像是用語法描述他的架構，所以跟真值表綜合出來的RTL View會有些許的不同，優點是可以不用思考太多直接用語法表達就好了。

module project1(
	input A,
	input B,
	input C,
	output reg  OUT1
);
wire [2:0] D;

assign D={A,B,C};

always@(*)begin
	case(D)
		0:begin OUT1=1'b0; end
		1:begin OUT1=1'b0; end
		2:begin OUT1=1'b0; end
		3:begin OUT1=1'b1; end
		4:begin OUT1=1'b0; end
		5:begin OUT1=1'b1; end
		6:begin OUT1=1'b1; end
		7:begin OUT1=1'b1; end
	endcase
end
endmodule

邏輯代數(Boolean algebra)

邏輯代數是利用真值表的輸出輸入，再用卡諾圖去做化簡，這樣可以完成＂最小化＂電路這件事情，在電路執行速度上會比＂非最小化＂電路快上不少，但多了需要卡諾圖化簡這一個步驟，有些麻煩。

module project1(

	input A,
	input B,
	input C,
	output OUT1
);

assign  OUT1=A&B |B&C|A&C;

endmodule

抽象描述(abstract description)

抽象描述是直接描述需要的＂行為＂，像是寫軟體一樣的思考方式，不用管真值表或是化簡代數，我只需要知道我要做的事情，像是三人裁判電路，我只需要知道「大於一人以上就輸出為真，其他為假」這一件事情，就能完成該電路描述，也是我們硬體描述語言工程師設計蠻常會使用的技巧，畢竟只描述行為的話，是不是就比還要看一堆圖表資料快多了呢！

module project1(

	input A,
	input B,
	input C,
	output reg  OUT1
);
wire[1:0]D;

assign D=A+B+C;

always@(D)begin
	if(D>1)begin
		OUT1=1; end
		else begin
		OUT1=0;
	end
end
endmodule

以上介紹三種描述方式，並不能說哪個比較優秀，只有在對的場合用對的描述方式，那麼那種描述方式就是最好的。以我個人來說，起初是擅長邏輯代數，後來了解語法候，用開始用描述＂結構＂的方式，更後來發現描述＂行為＂更為簡單，表達方式也是一步步進化出來的，都能熟練掌握才是好的，程式是死的，怎麼思考方面才是活的。

PS：三種表達方式的語法會有些微的差異，請注意這點。